本文共 622 字，大约阅读时间需要 2 分钟。

4月23日消息，国际研究机构Gartner发布最新云计算市场追踪数据，阿里云亚太市场排名第一，全球市场排名第三。阿里云亚太市场份额从26%上涨至28%，接近亚马逊和微软总和；全球市场份额从7.7%上涨至9.1%，进一步拉开与第四名谷歌差距，挤压亚马逊份额。

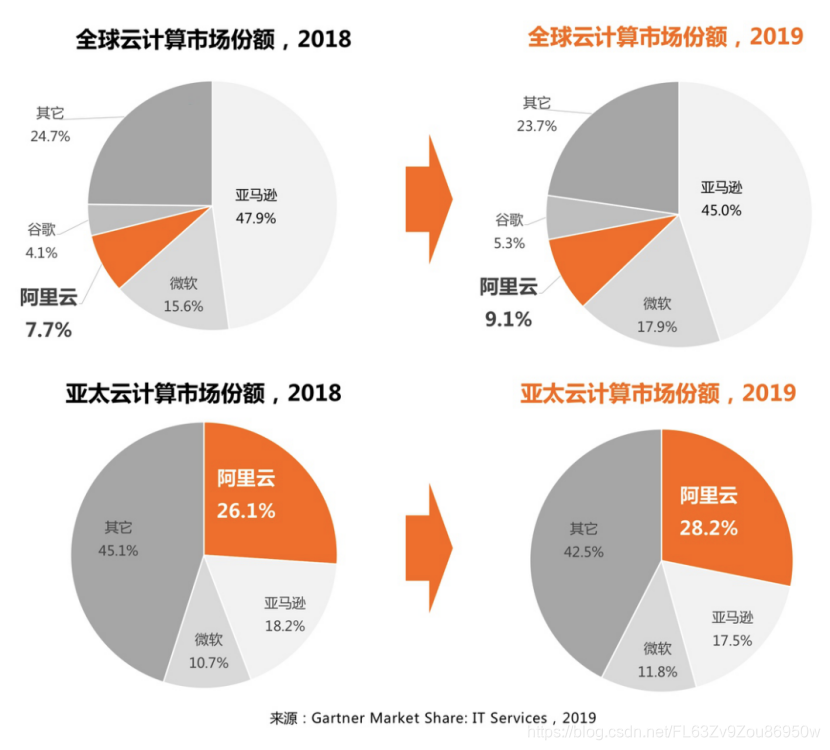
数据显示，2019年全球云计算IaaS市场持续快速增长，同比增长37.3%，总体市场规模达445亿美元。全球市场3A格局稳固，但亚马逊市场份额被微软和阿里云挤压，从2018年48%下降到45%。阿里云排名第三，市场份额增速最快，从2018年的7.7%，上涨至9.1%。

相比全球，亚太市场增长更快，云计算市场规模同比增长达50%。在亚太市场上，阿里云排名第一，市场份额进一步上涨，从2018年的26%上升至28.2%，接近亚马逊和微软总和。同期，亚马逊份额从去年18%下降至17%。

近日，阿里云宣布未来3年投入2000亿，用于云操作系统、服务器、芯片、网络等重大核心技术研发攻坚和面向未来的数据中心建设。3年再投2000亿意味着阿里云的数据中心和服务器规模再翻3倍，冲刺全球最大的云基础设施。

金融时报评论认为，阿里云近年来在中国市场份额不断稳固，2019年第四季度中国市场占比达46%。新冠疫情刺激了市场对远程工作背后的云基础设施与技术的需求，疫情之后，企业和机构将大幅加快上云脚步。

分析师普遍认为，阿里云进一步扩大云基础设施和核心技术投入，“未来数年内赶上亚马逊是大概率事件”。

转载地址：http://cbxe.baihongyu.com/